Normal and geodesic curvature
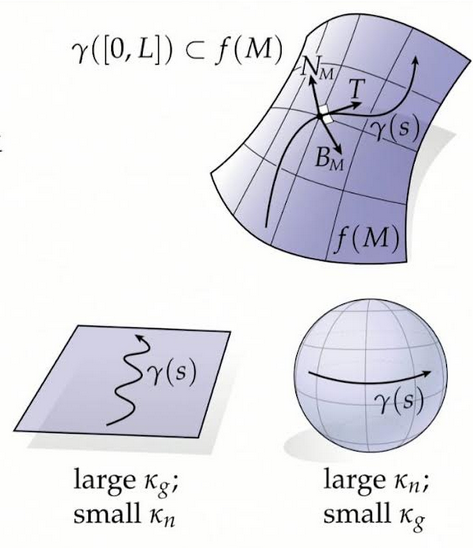
When we have a curve $\gamma:[0,L]\rightarrow \mathbb{R}^3$ contained in a immersed surface $f(M)$ we can define two notions related to the usual curvature of a curve and torsion of a curve. If we name $N_M$ to the unit normal to the surface and $B_M$ to the product $T\times N_M$, we can define:
- $\kappa_n:=\langle N_M, \frac{d}{ds}T\rangle$
- $\kappa_g:=\langle B_M, \frac{d}{ds}T\rangle$
Another approach (with other notation) (@needham2021visual page 116), if the curve is $C$ and the tangent vector at the point of study is $T$ we can consider the normal $n$ to the surface $S$, and the planes $T_pS$ (the tangent plane to $S$) and $\Pi_T$ the normal plane to the surface spanned by $T$ and $n$.
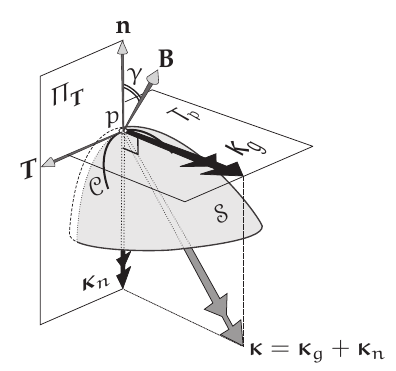
Suppose the osculating plane to $C$ at $p$ is inclined an angle $\gamma$ ($\gamma$ is the angle between the binormal $B$ of $C$ and the normal $n$ to $S$). Then $\kappa_n$ and $\kappa_g$ are the curvatures of the projections of $C$ onto $\Pi_T$ and $T_pS$ respectively. If the curvature of $C$ is $\kappa$ it is satisfied that
$$ \kappa_n=\kappa \mbox{sin}(\gamma) $$ $$ \kappa_g=\kappa \mbox{cos}(\gamma) $$Related to this notions is the Meusnier's theorem.
Intrinsic measurement of the geodesic curvature
As might be expected, the geodesic curvature can be obtained intrinsically. The inhabitants of the surface $S$ do not know that they live in a surface so they can try to measure the usual curvature by their own means, for example, by the measuring the change in the angle, as is outlined here.
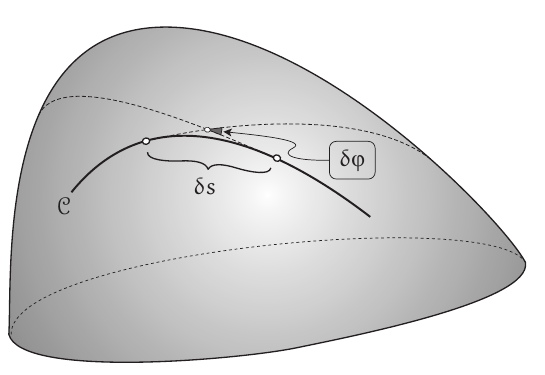
They weren't using tangent lines, indeed, but "tangent geodesics". The result is: what for them is the curvature, for us is the geodesic curvature.
See @needham2021visual page 119.
Relationship with covariant derivative
According to @needham2021visual page 243
$$ \nabla_v v=\kappa=\kappa_g+\kappa_n $$Defining the covariant derivative inherited from the ambient $\mathbb{R}^3$ as the projection on the tangent space to the surface in every point $D_v v=P[\nabla_v v]=\nabla_v v-(n\cdot \nabla_v v)n$ it turns out that
$$ \kappa_g=D_v v, $$since $\kappa_n=(n\cdot \nabla_v v)n$.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: